题面:https://codeforces.com/contest/807/problems
整场题目都是以CF为背景的,读题是个大问题,题意都不怎么好读懂。
最后发现是tourist出的场。
A. Is it rated?
题意:给定一个本次Round的榜,分别是比赛前的rating和比赛后的rating。要求你判断本次比赛是否rated。
解法:
如果前后的分数发生变化,则肯定rated。
再判断看是否有排在前面的人的rating比后面的低,如果有则肯定unrated。
(因为rated的话rating肯定会发生变化)
否则就是maybe。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
using namespace std;
pii a[2000];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
int mode = 0, unr = 0;
map<int, int> q;
for(int i = 0; i < n; i++)
{
cin >> a[i].first >> a[i].second;
if(a[i].second != a[i].first)
mode = 1;
}
if(mode)
cout << "rated" << endl;
else{
for(int i = 0; i < n - 1; i++)
if(a[i].first < a[i + 1].first)
unr = 1;
if(unr)
cout << "unrated" << endl;
else
cout << "maybe" << endl;
}
return 0;
}
B. T-Shirt Hunt
题意:题意不是很好懂。你有一个排名和分数,将你的分数做以下操作1
2
3
4i := (s div 50) mod 475
repeat 25 times:
i := (i * 96 + 42) mod 475
print (26 + i)
如果这$25$个数中有你的排名并且分数高于$y$,你就可以得到一件T-shirt.
你现在可以进行Hack来改变你的分数,hack成功一次加$100$分,失败扣$50$分
问你最少需要hack成功几次才能得到T-shirt。数据保证一定有解。
解法:暴力就好了呀。
首先考虑失败的hack一直减到小于$y$。
然后由于失败的hack不算次数,所以我们每次成功一次失败一次来使得一次可以增长$50$分。
最后处理一下,将增加的分数加$50$再除以$100$就能得到hack成功的次数了。
1 |
|
C. Success Rate
题意:你希望你在online judge上的准确率是$p/q$,现在你已经提交过$y$次,并且AC了$x$次。问你至少还需要提交几次才能达到$p/q$的准确率。你可以任意提交unsuccessful submissions或者successful submissions。给定$t$次query$(1 \leq t \leq 1000)$
解法:考虑二分。
首先考虑不可能的情况,如果想要准确率是100%和0%是比较困难的,不能考后期提交做到。直接判断看是否满足。
由于需要满足$\frac {p}{q} = \frac {x}{y}$,所以必然后续y一定是$q$的整数倍,以这样为单位,每次二分看能否满足要求。要求最后的X必须满足大于原先的AC题目数并且现在能够达到这么多的AC数量。
剩下的细节见代码。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
ll x, y, p, q;
cin >> x >> y >> p >> q;
if((p == q && x == y) || (p == 0 && x == 0))
{
cout << 0 << endl;
continue;
}
if((p == q && x != y) || (p == 0 && x != 0))
{
cout << -1 << endl;
continue;
}
// try to make x * q == p * y
ll l = 0, r = 1e10;
ll b = y / q * q;
if(y % q)
b += q;
for(int id = 0; id < 100; id++)
{
ll mid = (l + r) / 2;
ll temp = p * b / q + mid * p;//temp为AC的题目数
if(temp >= x && temp <= (x + mid * q + b - y))
r = mid;
/*要求满足大于原先的AC题目数并且现在能够达到这么多的AC数量*/
else
l = mid;
}
cout << b + r * q - y << endl;
}
return 0;
}
D. Dynamic Problem Scoring
题意:题意真的很难懂。(无限吐槽)过了几天我已经忘记这道题的题意了。
意思是有一张表,每道题目的最高分是由通过率决定的。通过率是指过的人数除以总人数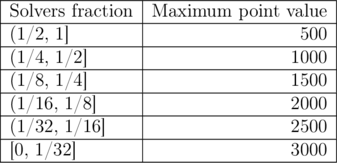
当然在不同时间过题,能获得的score也是不一样的。你在第$x$分钟过题,将会损失$(100 \cdot x / 250)% $的分数。你现在有一堆账号,可以任意提交对的或是错的答案。当然你必须得过了题目才能提交对的答案。以此来改变分值,问你是否能超过第二人的分数。
解法:其实就是暴力。
考虑策略,在什么情况下需要提高Max Point,什么情况下需要降低Max Point。
只有在两个人同时做出来了并且对方过的比我早的情况下才需要将交一堆正确答案以降低Max Point。其它情况下都是交一堆错的答案。
考虑什么情况下无解,由于$n$最大只有120。所以最多到达120 * 32,以后就不会有变化了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
using namespace std;
int t[200][10];
int solve[10], opr[10];
int per, cnt;
double score(int ac)
{
if(32 * ac <= per)
return 3000;
else if(16 * ac <= per)
return 2500;
else if(8 * ac <= per)
return 2000;
else if(4 * ac <= per)
return 1500;
else if(2 * ac <= per)
return 1000;
else
return 500;
}
inline double cal(int ac, double t)
{
return 1.0 * score(ac) * (1 - t / 250.0);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> per;
for(int i = 0; i < per; i++)
for(int j = 0; j < 5; j++)
{
cin >> t[i][j];
if(t[i][j] != -1)
solve[j]++;
}
double s1 = 0, s2 = 0;
for(int i = 0; i < 5; i++)
{
if(t[0][i] != -1)
s1 += cal(solve[i], t[0][i]);
if(t[1][i] != -1)
s2 += cal(solve[i], t[1][i]);
if(t[0][i] != -1 && t[1][i] != -1 && (t[0][i] > t[1][i]))
opr[i] = 1;
}
while(s1 <= s2)
{
s1 = 0, s2 = 0;
cnt++, per++;
for(int i = 0; i < 5; i++)
{
solve[i] += opr[i];
if(t[0][i] != -1)
s1 += cal(solve[i], t[0][i]);
if(t[1][i] != -1)
s2 += cal(solve[i], t[1][i]);
}
if(cnt == 4000)
{
cout << -1 << endl;
return 0;
}
}
cout << cnt << endl;
return 0;
}