LeetCode142 环形链表II

链接：https://leetcode-cn.com/problems/linked-list-cycle-ii/

题意

给定一个链表，要求判断链表是否存在环，如果存在找出其中环的起点。
快慢指针的巧妙运用。已知快慢指针判断链表是否有环，只需要找到判两个指针是否相遇。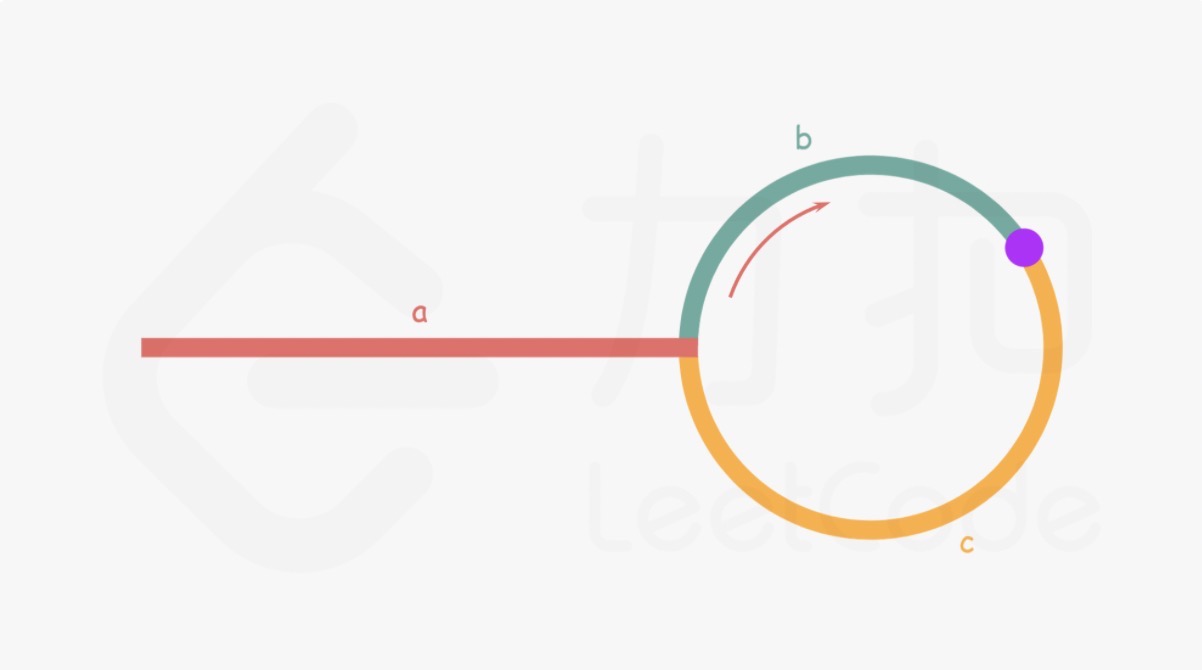


设链表中环外部分的长度为 a。slow 指针进入环后，又走了b的距离与fast相遇。此时，fast指针已经走完了环的n圈，因此它走过的总距离为

$$a+n(b+c)+b=a+(n+1)b+nca+n(b+c)$$

由于fast指针走过的距离都为slow指针的2倍，于是有

$$a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)$$

我们会发现：从相遇点到入环点的距离加上 n-1n−1 圈的环长，恰好等于从链表头部到入环点的距离。

解法

当 slow 和 fast 第一次相遇时，我们将 fast 重新移动到链表开头，并让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时，相遇的节点即为环路的开始点。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == NULL || head -> next == NULL) return NULL;
        ListNode *p_slow = head -> next;
        ListNode *p_fast = p_slow -> next;
        while(p_fast != NULL && p_slow != p_fast) {
            p_slow = p_slow -> next;
            p_fast = p_fast -> next;
            if(p_fast != NULL) {
                p_fast = p_fast -> next;
            }
        }
        if (p_fast == NULL) return NULL;
        p_fast = head;
        while(p_fast != p_slow){
            p_fast = p_fast -> next;
            p_slow = p_slow -> next;
        }
        return p_slow;
    }
};