题面:http://codeforces.com/contest/791/problems
A. Bear and Big Brother
题意:一个数第二天是第一天的3倍,另一个数第二天是第一天的2倍,问什么时候第一个数大于第二个数。
解法:模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
using namespace std;
const int maxn = 1e4;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int a, b;
cin >> a >> b;
for(int i = 1; i <= 100; i++)
{
a *= 3;
b *= 2;
if(a > b)
{
cout << i << endl;
break;
}
}
return 0;
B. Bear and Friendship Condition
题意:如果A和B是好朋友,B和C是好朋友,则要求A和C必须是好朋友。称之为“好朋友定则”
给定一些朋友的关系,如果这堆朋友间的关系满足好朋友定则,则输出“YES”,否则“NO”
解法:并查集+完全图性质
很显然的是对于一个好朋友团体,其中的每两个人之间都必须要有一条边相连,即完全图。
对于一个n个人的团队,边数就是$\frac {n * (n - 1)}{2}$条。
首先并查集处理,对于每个团队计算完全图所需要的边数相加,和输入的边数比较即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
using namespace std;
const int maxn = 2e5;
vector<int> g[maxn];
int par[maxn];
int F(int x)
{
if(x == par[x])
return x;
return par[x] = F(par[x]);
}
void unite(int a, int b)
{
a = F(a);
b = F(b);
par[a] = b;
}
void init(int n)
{
for(int i = 1; i <= n; i++)
par[i] = i;
}
ll clu[maxn];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
init(n);
for(int i = 0; i < m; i++)
{
int a, b;
cin >> a >> b;
unite(a, b);
}
for(int i = 1; i <= n; i++)
clu[F(i)]++;
ll sum = 0;
for(int i = 1; i <= n; i++)
{
sum += clu[i] * (clu[i] - 1) / 2;
}
if(sum == m)
cout << "YES" << endl;
else
cout << "NO" << endl;
return 0;
}
C. Bear and Different Names
题意:n个字符串的序列,连续的m个的一个group中如果有任意两个相同的则为no,如果没有相同的为yes。现在告诉你这$n-m+1$(起始分别为第1个,第2个…第n-m+1个)group分别是yes还是no 需要你构造出这n个字符串
解法:贪心 思维
我们可以考虑对于任意的一个group,如果不存在名字相同的,下一个需要存在名字,则将下一个名字取为当前的第一个即可。因为下次的group里不存在第一个。
所以每次只要考虑最后一个。如果是yes,则产生一个新名字,否则最后一个==第一个名字。
新名字很容易构造。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
using namespace std;
vector<string> ans;
vector<string> name;
void getname()
{
for(int i = 0; i < 26; i++)
for(int j = 0; j < 26; j++)
{
string t = "A";
t[0] += i;
t += j + 'a';
name.push_back(t);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
getname();
int idx = 0;
for (int i = 1; i < m; i++)
ans.push_back(name[idx++]);
for (int i = m; i <= n; i++)
{
string t;
cin >> t;
if(t[0] == 'N')
ans.push_back(ans[i - m]);
else
ans.push_back(name[idx++]);
}
for(auto idx: ans)
cout << idx << ' ';
cout << endl;
return 0;
}
D. Bear and Company
题意:有一个人喜欢在树上跳来跳去的,每次能跳$k$步$(0 < k <= 5)$, 问你它要把所有点对跳一遍需要跳多少次。
准确一点的说法:
For a pair of vertices$ (s,t)$ we define $f(s,t)$ as the minimum number of jumps Limak needs to get from s to t. Your task is to find the sum of $f(s,t)$ over all pairs of vertices $(s,t)$ such that $s < t$.
解法:树形dp
首先考虑一种简单的情况,如果每次只能跳一步,那么就是计算所有点对的距离和。
这是一个简单基础经典的树形dp。
我们考虑计算每条边的贡献,对于一条边u->v假设u的一侧有m个结点,v的一侧有n个结点,那么这两边的结点要想互通,必然要经过这一条边,所以这一条边的贡献就是m乘以n。所以我们只需要一遍dfs,计算出每条边的贡献和即可。
具体来说,我们需要记录每个结点为根的子树所含结点$i$个,那么另一侧的结点个数必然是$n-i$个,每次相加即可。
杭电2376这样就可以了。
但是对于这道题目而言,不能直接将所有点对的距离和相加除以k,因为存在两个结点的距离为10,比如k为3,但一定是要跳至少4次。故我们需要进行补全,将每个点对距离补全为k的倍数加到最终的答案里去。
这道题理解还是比较困难的,想了一天才想明白(菜啊)
看了题解说要求每个点对需要补全的距离一直不能理解是怎么求出来的。
任意两个点的距离等于两个点的深度和减去LCA的深度。题解中巧妙的将节点按层次进行分类。用dp[i][j]表示以i为根的子树的所有结点中到root节点距离(深度)%k为j的节点个数这个的理解花了我很长的时间。
由于我们只需要计算两个节点距离补全成k所需要的次数,所以我们只需要枚举二重循环,枚举当前结点和其子结点的所有深度,计算其各有多少个结点。又由于直接处理结点的直接后继,LCA就是当前结点,深度就是DFS当前深度。
举个例子:k = 2
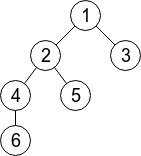
对于这棵树,我们观察2号结点,假设现在4.5号子树已经遍历完成,5号子树正回溯回来。
则dp[2][0] = 1,dp[2][1] = 2,dp[5][0]=1
处理的其实是2->5, 4->5, 6->5, 其距离%k后分别是1, 0, 1,ans需要加上1, 0, 1。
对于每次DFS,我们需要做的是计算子树中的每个点相互到达所需要加的值,处理完还要把子树的dp值继承给父结点以进行其他点对的计算。
See my code for details.好好理解.
1 |
|